How to use Row Echelon Form in Finding Determinant of a 3x3 Matrix

-

Calculation of 3x3 matrix determinant by Row Echelon Form


About the method (Gaussian Elimination)
To calculate a determinant you need to do the following steps:

  1. Set the matrix (must be square)

  2. Reduce this matrix to row echelon form using elementary row operations so that all the elements below the diagonal are zero.

  3. Multiply the main diagonal elements of the matrix - determinant is calculated.

Example 1. Find the determinant of matrix A.

                                                    

Solution:


Eliminate elements in the 1st column under the 1st element.

Eliminate elements in the 2nd column under the 2nd element.

Multiply the main diagonal elements.

                                                            

Example 2. Find the determinant of matrix B.

                                                

Solution:

Eliminate elements in the 1st column under the 1st element.

Eliminate elements in the 2nd column under the 2nd element.

Multiply the main diagonal elements.

                                                                



| BS in Math | MS in Applied Math (30-units earned) | MS in Pure and Applied Math (Thesis still on progress) | Full-time Private Tutor | Online Math Instructor |

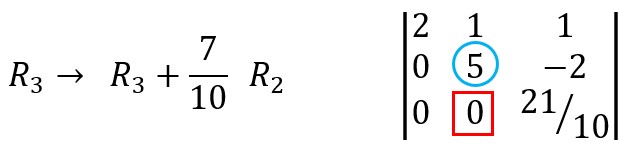
Comments

Post a Comment

Popular posts from this blog

How to use Triangle's Rule in Finding Determinant of a 3x3 Matrix

-
Image
Calculation of a 3x3 matrix determinant using Triangle's Rule. The Triangle’s rule will be formed with this scheme:                                                 The product of diagonal elements and product of elements in the both vertex of two triangles of the first determinant get the “+” sign and the product of diagonal elements and product of elements in the both vertex of two triangles of the second determinant get the “-” sign. In base of triangle’s rule, we have: This method is somehow similar to  Sarrus Rule .
Read more

How to use Co-factor Expansion along the Column in Finding Determinant of a 3x3 Matrix

-
Image
Calculation of 3 ✖ 3 matrix determinant by  Co-factor Expansion along the Column The Co-Factor Expansion Definition : If  A   is a square matrix then the minor of  A ij , denoted by  M ij , which is the determinant of the sub-matrix that results from removing (deleting) the row  ith   and  jth  column of   A . Sign Chart for a 3×3 determinant                                                      A sign chart is either a + or - for each element in the matrix. The first element (row 1, column 1) is always a + and it alternates from there. Note:  The + does not mean positive and the - negative. The + means the same sign as the minor and the - means the opposite of the minor. Think of it as addition and subtraction rather than positive or negative. About the Method To calculate a determinant you need to do the following steps:   1. Pick any column of the matrix 2. Find all the cofactors for that column 3. Multiply each cofactor by its matrix entry 4. Add all the values you've gotten.  
Read more