How to use Sarrus Rule in Finding Determinant of a 3x3 Matrix
Calculation of a 3x3 matrix determinant using Sarrus Rule.
Sarrus' Rule or Sarrus' Scheme
is a method and a memorization scheme to compute the determinant of a matrix.
It is named after the French mathematician Pierre Frédéric Sarrus. There are
four Sarrus’s rules or Sarrus’ schemes to compute the determinant
of a matrix.
Sarrus’ scheme 1:
Consider an arbitrary 3x3 matrix A=[aij]. The determinant of A is defined as follows:

Sarrus’ scheme 2:
Write
out the 2 columns (2nd and 3rd column) of the matrix to
the left of the matrix, so that you have a total of 5 columns. Then add the
products of the diagonals going from top to bottom and subtract the products of
the diagonals going from bottom to top. These yields
Example 2. Find the determinant of matrix B using Sarrus Scheme 2.
Solution:
Sarrus’ scheme 3:
Write out the first 2 rows of the matrix to the bottom of the 3rd row, so that you have a total of 5 rows. Then add the products of the diagonals going from top to bottom and subtract the products of the diagonals going from bottom to top. These yields
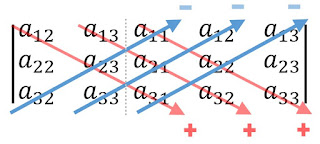
Sarrus’ scheme 4:
Write out the 2 rows (2nd and 3rd rows) of the matrix to the above of the 1st row, so that you have a total of 5 rows. Then add the products of the diagonals going from top to bottom and subtract the products of the diagonals going from bottom to top. These yields
Example 2. Find the determinant of matrix B using Sarrus Scheme 4.
Solution:










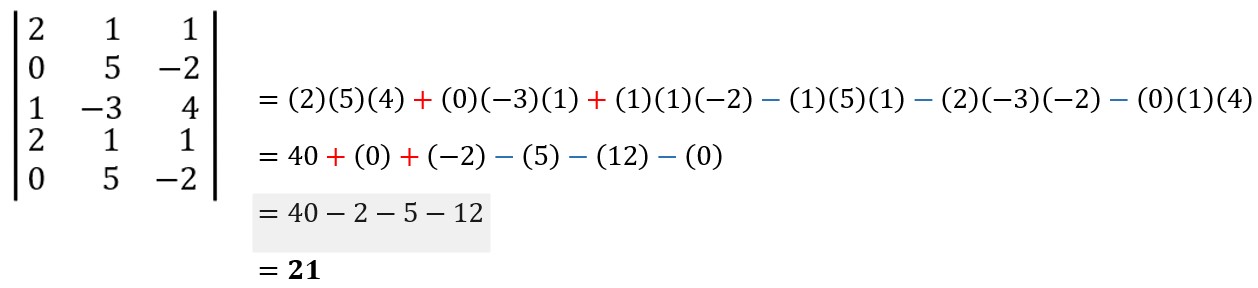


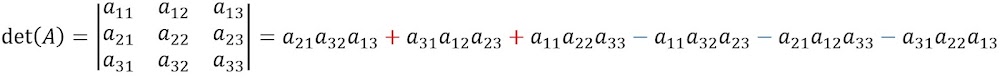




Comments
Post a Comment