What is Determinant of a matrix? How to calculate determinant of Order 1, 2, 3 and arbitrary Order? What are the Properties of Determinants?
Determinants
Introduction
Each n-square matrix A =[aij]is assigned a special scalar called the determinant of A, denoted by det (A) or |A|or An n✕n array of scalars enclosed by straight lines, called
a determinant
of order n, is not a matrix but denotes the determinant of the enclosed
array of scalars, i.e., the enclosed matrix.
The determinant function was
first discovered during the investigation of systems of linear equations. The
determinant is an indispensable tool in investigating and obtaining properties
of square matrices.
Determinants of Order 1 and 2
The Determinants of Order 1 and 2 are defined as follows:
The determinant of a 1x1 matrix A =[a11] is the scalar a11 itself, that is,
The determinant of order two may easily
remembered by using the following diagram:
That is, the determinant is equal to the product of the elements along the one
plus-labeled arrow minus the product of the elements along the one
minus-labeled arrow.
Example 1: Find the determinant of matrix A.
Solution:
Example 2: Find the determinant of matrix B.
Solution:
Determinants of Order 3
There are many ways on finding the determinant of a 3x3 matrix.
To calculate the determinant of a 3x3 matrix, click the following:
Sarrus Rule
Triangle's Rule
Co-Factor Expansion along the Column
Co-Factor Expansion along the Row
Row Echelon Form
Properties of Determinants
Theorem: The determinants of a matrix A and its transpose Aᵀ are equal, that is,
Theorem: The determinants of a matrix A and its transpose Aᵀ are equal, that is,


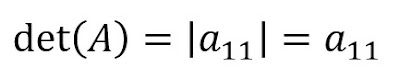








Comments
Post a Comment